Entropie conjointe \(H(X,Y)\) de \(X\) et \(Y\)
Quantité définie par : $$H(X,Y)=-\sum_{x\in\mathcal X}\sum_{y\in\mathcal Y}p_{XY}(x,y)\log_2(p_{XY}(x,y))$$
- correspond à l'Information apportée par le système \((X,Y)\)
- \(H\) est positive et symétrique
- \(H(X,Y)\leqslant\) \(H(X)+H(Y)\), avec égalité si et seulement si \(X\) et \(Y\) sont indépendantes
- \(H(X,Y)\geqslant\) \(\max(H(X),H(Y))\) avec égalité si et seulement si les deux sources contiennent exactement la même Information
- formule à partir de l'Entropie conditionnelle : \(H(X,Y)=H(X)+H(Y|X)\)
- ce concept peut être étendu à \(n\) variables, avec la formule : $$H(X_{1:n})=\sum^n_{i=1}H(X_i|X_{1:i-1})$$
- on a la majoration \(H(X_{1:n})\leqslant\) \(\sum^n_{i=1}H(X_i)\)
Questions de cours
START
Ω Basique (+inversé optionnel)
Recto: Comment représenter l'entropie conjointe \(H(X,Y)\) sur un diagramme de Venn ?
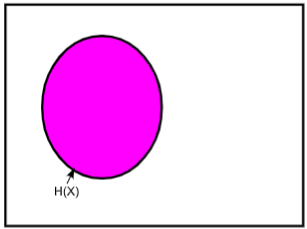
Verso:
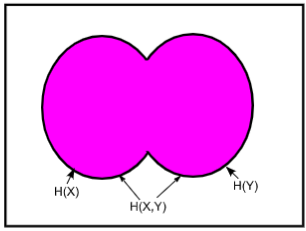
Bonus:
Carte inversée ?:
END

